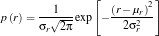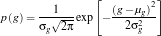Linear discriminant analysis is a classification technique by which one creates a discriminant function from predictor variables.
In discriminant analysis, there is a dependent variable (Y) which is the group and the independent variables (X) which are the object features that might describe the group. If the groups are linearly separable, then we can use linear discriminant analysis. This method suggests that the groups can be separated by a linear combination of features that describe the objects.
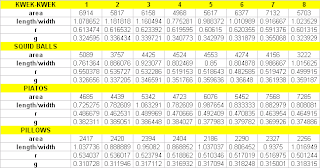
In this activity, i used LDA to classify pillows (chocolate-coated snack) and kwek-kwek (orange, flour-coated quail egg) based on the features such as pixel area, length-to-width ratio, average red component (NCC), and average green component (NCC).
In discriminant analysis, there is a dependent variable (Y) which is the group and the independent variables (X) which are the object features that might describe the group. If the groups are linearly separable, then we can use linear discriminant analysis. This method suggests that the groups can be separated by a linear combination of features that describe the objects.
In this activity, i used LDA to classify pillows (chocolate-coated snack) and kwek-kwek (orange, flour-coated quail egg) based on the features such as pixel area, length-to-width ratio, average red component (NCC), and average green component (NCC).


Images of the two samples were taken using Olympus Stylus 770SW. The images are then white balanced using reference white algorithm with the white tissue as the reference. This is to maintain uniform tissue color in each of the images. The images are then cut such that a single image contains a single sample. Features are then extracted from each of the cut images in the same manner as the previous activity.
The data set is again divided into training and test sets, with the first four images of each sample comprising the training set while the last four images for the test set.
Following the discussion and equations from Pattern_Recognition_2.pdf by Dr. S. Marcos, I computed the following values.
The data set is again divided into training and test sets, with the first four images of each sample comprising the training set while the last four images for the test set.
Following the discussion and equations from Pattern_Recognition_2.pdf by Dr. S. Marcos, I computed the following values.

An object is assigned to a class with the highest f value. As can be seen from the table below, most of group 1 (pillows) have higher f1 values while those in group 2 (kwek-kwek) have higher f2 values. 100% classification is obtained.
---
//code
TRpillow=fscanfMat('TrainingSet-Pillows.txt');
TSpillow=fscanfMat('TestSet-Pillows.txt');
TRkwek=fscanfMat('TrainingSet-Kwekkwek.txt');
TSkwek=fscanfMat('TestSet-Kwekkwek.txt');
TRpillow=TRpillow';
TSpillow=TSpillow';
TRkwek=TRkwek';
TSkwek=TSkwek';
TRpilmean=mean(TRpillow,1);
TRkwekmean=mean(TRkwek,1);
globalmean=(TRpilmean+TRkwekmean)/2;
globalmean=mtlb_repmat(globalmean,4,1);
TRpillow=TRpillow-globalmean;
TRkwek=TRkwek-globalmean;
c_pil=((TRpillow')*TRpillow)/4;
c_kwek=((TRkwek')*TRkwek)/4;
C=((4*c_pil)+(4*c_kwek))/8;
P = [0.5;0.5];
for i=1:4
f1(i) = (TRpilmean*inv(C)*(TSkwek(i,:)'))-((0.5)*(TRpilmean)*inv(C)*(TRpilmean')+log(P(1)));
f2(i) = (TRkwekmean*inv(C)*(TSkwek(i,:)'))-((0.5)*(TRkwekmean)*inv(C)*(TRkwekmean')+log(P(2)));
end
//end code
---
Thanks Jeric Tugaff for the tips and discussions and Cole Fabros for the images of the sample.
---
Rating 8.5/10 since I implemented and understood the technique correctly but was late in posting this blog entry.
//code
TRpillow=fscanfMat('TrainingSet-Pillows.txt');
TSpillow=fscanfMat('TestSet-Pillows.txt');
TRkwek=fscanfMat('TrainingSet-Kwekkwek.txt');
TSkwek=fscanfMat('TestSet-Kwekkwek.txt');
TRpillow=TRpillow';
TSpillow=TSpillow';
TRkwek=TRkwek';
TSkwek=TSkwek';
TRpilmean=mean(TRpillow,1);
TRkwekmean=mean(TRkwek,1);
globalmean=(TRpilmean+TRkwekmean)/2;
globalmean=mtlb_repmat(globalmean,4,1);
TRpillow=TRpillow-globalmean;
TRkwek=TRkwek-globalmean;
c_pil=((TRpillow')*TRpillow)/4;
c_kwek=((TRkwek')*TRkwek)/4;
C=((4*c_pil)+(4*c_kwek))/8;
P = [0.5;0.5];
for i=1:4
f1(i) = (TRpilmean*inv(C)*(TSkwek(i,:)'))-((0.5)*(TRpilmean)*inv(C)*(TRpilmean')+log(P(1)));
f2(i) = (TRkwekmean*inv(C)*(TSkwek(i,:)'))-((0.5)*(TRkwekmean)*inv(C)*(TRkwekmean')+log(P(2)));
end
//end code
---
Thanks Jeric Tugaff for the tips and discussions and Cole Fabros for the images of the sample.
---
Rating 8.5/10 since I implemented and understood the technique correctly but was late in posting this blog entry.