In this activity, we use color as a feature for segmenting images. To do so, we first transform the color image's RGB into rgI. rgI is part of the normalized chromaticity coordinates or NCC color space. This color space separates chromaticity (r g) and brightness (I) information.
Per pixel, let I = R+G+B. Then the normalized chromaticity coordinates are
r = R/I
g = G/I
b = B/I
g = G/I
b = B/I
---

*http://images.replacements.com/images/images5/china/H/homer_laughlin_fiesta_shamrock_green_mug_P0000201549S0044T2.jpg
---
Parametric Probability Distribution
Shown below is the cropped region of the colored image, wherein we get the mean and standard deviation for both r and g so as to get the probability that a certain pixel belongs to the ROI.

We perform this over all pixels and plot the probability that a pixel belongs to our ROI.
Here's the distribution

And here's the segmented image, wherein the white parts corresponds to the pixels belonging to the ROI according to our Gaussian PDF.

---
Nonparametric Segmentation (Histogram Backprojection)

and the corresponding segmented image

Nonparametric image segmentation produced better results as compared to the parametric segmentation. Also, in nonparametric segmentation, we never assumed normality of distribution of the r and g, thus, this method is more accurate as compared to parametric segmentation.

*http://images.replacements.com/images/images5/china/H/homer_laughlin_fiesta_shamrock_green_mug_P0000201549S0044T2.jpg
---
Parametric Probability Distribution
Segmentation based on color can be performed by determining the probability that a pixel belongs to a color distribution of interest. This implies that the color histogram of the region of interest must first be extracted. To do so, one crops a subregion of the ROI and compute the histogram from it. The histogram when normalized by the number of pixels is already the probability distribution function (PDF) of the color. To tag a pixel as belonging to a region of interest or not is to find its probability of belonging to the color of the ROI. Since our space is r and g we can have a joint probability p(r) p(g) function to test the likelihood of pixel membership to the ROI. We can assume a Gaussian distribution independently along r and g, that is, from the r-g values of the cropped pixel we compute the mean μr , μg and standard deviation σr , σg from the pixel samples. The probability that a pixel with chromaticity r or g belongs to the ROI is then
The joint probability is just the product of p(r) and p(g).
Shown below is the cropped region of the colored image, wherein we get the mean and standard deviation for both r and g so as to get the probability that a certain pixel belongs to the ROI.

We perform this over all pixels and plot the probability that a pixel belongs to our ROI.
Here's the distribution

And here's the segmented image, wherein the white parts corresponds to the pixels belonging to the ROI according to our Gaussian PDF.

---
Nonparametric Segmentation (Histogram Backprojection)
In non-parametric estimation, the histogram itself is used to tag the membership of pixels. Histogram backprojection is one such technique where based on the color histogram, a pixel location is given a value equal to its histogram value in chromaticity space.
Here's the histogram used

and the corresponding segmented image

Nonparametric image segmentation produced better results as compared to the parametric segmentation. Also, in nonparametric segmentation, we never assumed normality of distribution of the r and g, thus, this method is more accurate as compared to parametric segmentation.
---
Reference:
Activity 16 Lecture Handouts by Dr. Maricor Soriano.
Reference:
Activity 16 Lecture Handouts by Dr. Maricor Soriano.
---
Thanks to Ed for the valuable discussions and arguments with regards to the technique.
---
I give myself a 10 for I implemented image segmentation quite well. :)
Thanks to Ed for the valuable discussions and arguments with regards to the technique.
---
I give myself a 10 for I implemented image segmentation quite well. :)
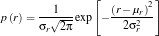
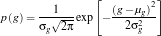

1 comment:
seriously interesting stuff.....
what exactly are you doing with this information?
Post a Comment